Da unser Kosmos im Großen und Ganzen elektrisch neutral ist und die Quantenchromodynamik nur auf sehr kurzen Entfernungen wirkt, folgt jedwede Bewegung auf kosmischem Maßstab allein den Gesetzen der Gravitation. Wir schauen in die ferne Zukunft. Irgendwann wird jede, auch unsere Sonne, ihren nuklearen Brennstoff verbraucht haben. Abhängig von ihrer Masse bildet sich ein zunächst stabiler Endzustand aus: ein harter Brocken aus normaler Materie, im wesentlichen Eisen, ein Neutronenstern oder ein schwarzes Loch. Letztlich unerheblich, denn die kosmische Nachbarschaft spürt nur, wie die verbliebene Masse die Raumzeit deformiert. Gravitativ gebundene kosmische Systeme, so auch zum Beispiel unsere lokale Galaxiengruppe, werden aufgrund ihrer Massen kontrahieren. Letztlich wird jede Masse in einer sehr langsamen spiralförmigen Bewegung dem nächstgelegenen schwarzen Loch zustreben und dabei Gravitationswellen aussenden: unsere Sonne verschwindet im schwarzen Loch des galaktischen Zentrums der Milchstraße. Die Milchstraße kollabiert mit Andromeda, und deren zentrales schwarzes Loch wird zwangsläufig seinen Partner spüren und den geometrodynamischen Spiraltanz beschleunigen, der schließlich zur Vereinigung führen muss. Irgendwann wird auch die letzte Masse und das letzte schwarze Loch unserer lokalen Gruppe diesen Weg gegangen sein, und von Allem wird nur noch ein sehr großes finales schwarzes Loch in einem ewig expandierenden Kosmos verbleiben, wo weit entfernt andere Galaxiencluster ein ähnliches Ende nehmen. Sieht so das Ende aus, auf immer auseinandereilende schwarze Löcher als Überbleibsel ehemals gravitativ gebundener Galaxiencluster? Ein Haufen versprengter Singularitäten, die dem Kosmos als Entropiestaubsauger eine kurze Phase bunter Evolution geschenkt haben, indem sie lokale Nichtgleichgewichtssysteme befeuerten und ihnen ein kurzes verschwenderisches Dasein erlaubten. Jetzt, wo jedwede Masse in Singularitäten gestürzt oder ins Unendliche enteilt ist, sind alle gravitativen Freiheitsgrade erschöpft: die kosmische Entropie kann nicht mehr wachsen! Der zweite Hauptsatz hat alles Geschehen zum Stillstand gebracht. Das ewig-langweilige Ende?
Nicht alles Geschehen steht: die Expansion des leeren Kosmos setzt sich schließlich fort, und da der leere Kosmos noch immer mit der vom Urknall geerbten Hintergrundstrahlung erfüllt ist, sinkt deren Temperatur proportional zur Ausdehnung des Kosmos und wird dem absoluten Nullpunkt immer näherkommen. Was passiert nun mit den schwarzen Löchern in einem immer kälter werdenden Kosmos? Zunächst einmal nichts, denn neue Nahrung gibt es nicht, so dass sie nicht mehr wachsen können und nur mehr auseinanderstreben.
Ein Ende allen Seins in schwarzen Löchern? Wir versuchen, das Verhalten von schwarzen Löchern zu verstehen. Raum ist Gravitation und fließt mit ihr. Die Wirkung der Gravitation muss wegen der Energieerhaltung im gleichen Maße abnehmen, wie der Raum zunimmt. Im einfachsten Fall einer kleinen Punktmasse ist der Raum Euklidisch und seine Kugelfläche wächst mit ![]() . Also muss die Wirkung der Gravitation, ihre Anziehungskraft, mit
. Also muss die Wirkung der Gravitation, ihre Anziehungskraft, mit ![]() fallen.
fallen.
Mit[1]
![]() muss jede Aggregation von Massen M zu
einem schwarzen Loch führen, wenn sie nur genügend lange fortgesetzt wird.
Schließlich wächst die Masse einer Kugel mit
muss jede Aggregation von Massen M zu
einem schwarzen Loch führen, wenn sie nur genügend lange fortgesetzt wird.
Schließlich wächst die Masse einer Kugel mit ![]() ,
sodass die Kraft an ihrer Oberfläche auf einen Probekörper m infolge einer
Aggregation mit
,
sodass die Kraft an ihrer Oberfläche auf einen Probekörper m infolge einer
Aggregation mit ![]() wächst und irgendwann
selbst die stärkste Materie zum Einsturz bringen muss. Alle Materie kollabiert
in eine Singularität, die sich mit einem Ereignishorizont umgibt: wer einem
Sturz ins schwarze Loch dort noch entkommen will, muss bereits seine gesamte
Energie zur Flucht aufwenden! Photonen entweichen gerade noch, erreichen aber
den freien Raum in weiter Ferne nur noch unendlich rotverschoben und mit
verschwindender Frequenz. Die Fluchtgeschwindigkeit massiver Teilchen ist die
des Lichts.
wächst und irgendwann
selbst die stärkste Materie zum Einsturz bringen muss. Alle Materie kollabiert
in eine Singularität, die sich mit einem Ereignishorizont umgibt: wer einem
Sturz ins schwarze Loch dort noch entkommen will, muss bereits seine gesamte
Energie zur Flucht aufwenden! Photonen entweichen gerade noch, erreichen aber
den freien Raum in weiter Ferne nur noch unendlich rotverschoben und mit
verschwindender Frequenz. Die Fluchtgeschwindigkeit massiver Teilchen ist die
des Lichts.
[1]
Zur Vereinfachung der Schreibweise verwenden wir im Folgenden universelle Einheiten.
Damit bekommen Lichtgeschwindigkeit ![]() , Gravitationskonstante
, Gravitationskonstante ![]() , Entropiequotient
, Entropiequotient
![]() und Wirkungsquantum
und Wirkungsquantum ![]() den Wert
den Wert ![]() .
.
Nehmen wir für eine ‚heuristische‘ Betrachtung die klassische Formel für die Fluchtgeschwindigkeit[1] ![]() und setzen diese gleich der Lichtgeschwindigkeit: aus
und setzen diese gleich der Lichtgeschwindigkeit: aus ![]() folgt mit
folgt mit ![]() (universelle Einheiten!)
(universelle Einheiten!) ![]() und damit
und damit ![]() .
.
[1]
Mit der Fluchtgeschwindigkeit gleicht die kinetische der potentiellen Energie
und es gilt ![]()
Lässt man ein massives Teilchen (einen
Probekörper) langsam zu einem schwarzen Loch hinab, so lässt sich seine gesamte
Ruhemasse als Energie gewinnen und aus dem System ‚Schwarzes Loch +
Probekörper‘ herausziehen: Mit dem Überschreiten des Ereignishorizonts hat
sich die Masse des Systems von vordem ![]() auf nunmehr nur noch
auf nunmehr nur noch ![]() reduziert.
reduziert.
Wir betrachten das Verschwinden eines ‚kleinen‘ Probekörpers in einem schwarzen Loch und nehmen an, er sei leichter als eine universelle Einheitsmasse, also kleiner als ![]() . Ein kleiner Papierschnitzel würde reichen. Dann ist seine durch die Massenwellenlänge[1]
. Ein kleiner Papierschnitzel würde reichen. Dann ist seine durch die Massenwellenlänge[1] ![]() gegebene Ortsunschärfe bereits größer als sein Ereignishorizont (für die universelle Einheitsmasse ist beides gleich). Wir heben den Probekörper vom Ereignishorizont um eine halbe Ortsunschärfe
gegebene Ortsunschärfe bereits größer als sein Ereignishorizont (für die universelle Einheitsmasse ist beides gleich). Wir heben den Probekörper vom Ereignishorizont um eine halbe Ortsunschärfe ![]() in die Höhe und leisten dabei die Hubarbeit
in die Höhe und leisten dabei die Hubarbeit ![]() . Dabei haben wir den oben gefundenen Zusammenhang
. Dabei haben wir den oben gefundenen Zusammenhang ![]() verwendet. Interessanterweise ist die Hubarbeit von m unabhängig, solange die Masse nur genügend kein ist: Je kleiner die Masse m, desto größer seine Massenwellenlänge
verwendet. Interessanterweise ist die Hubarbeit von m unabhängig, solange die Masse nur genügend kein ist: Je kleiner die Masse m, desto größer seine Massenwellenlänge ![]() , das Produkt von Kraft mal Weg und damit die Hubarbeit ist konstant!
, das Produkt von Kraft mal Weg und damit die Hubarbeit ist konstant!
[1] Die Massenwellenlänge
![]() ist ein Maß für die Ortsunschärfe
aufgrund der quantenmechanischen Wellennatur des Teilchens. Sie erscheint zB in
der relativistischen Wellengleichung für
Bosonen
ist ein Maß für die Ortsunschärfe
aufgrund der quantenmechanischen Wellennatur des Teilchens. Sie erscheint zB in
der relativistischen Wellengleichung für
Bosonen ![]()
An dieser Stelle[1] wissen wir nicht, ob der Probekörper bereits hinter dem Ereignishorizont verschwunden ist. Das System besitzt eine Unsicherheit, ein minimales Nichtwissen: ist das Teilchen noch da, oder ist es bereits verschwunden? Die damit verbundene minimale Information ist 1 Bit, und auch die damit verbundene Entropie hat den Wert 1. Mit dem Verschwinden des Probekörpers hinter dem Ereignishorizont des schwarzen Lochs wächst unser Wissen um ein Bit und die Entropie sinkt um 1. Da aber die Entropie nur wachsen, niemals aber sinken kann, hat die Entropie des schwarzen Lochs um eine Einheit zugenommen. Gleichzeitig muss die Energie E des schwarzen Lochs um die Hubarbeit, also den Wert ![]() zugenommen haben.
zugenommen haben.
[1] Eine halbe Ortsunschärfe über dem Ereignishorizont
Wir haben also folgendes Ergebnis:
Mit dem Verschwinden einer kleinen Probemasse
m hinter dem Ereignishorizont eines schwarzen Lochs wächst dessen Energie um ![]() , also dessen Radius
, also dessen Radius ![]() um
um ![]() , und damit wächst die Oberfläche
, und damit wächst die Oberfläche ![]() um den Wert
um den Wert ![]() . Damit[5] ist
. Damit[5] ist ![]() : die Entropie wächst proportional mit der Oberfläche
eines schwarzen Lochs!
: die Entropie wächst proportional mit der Oberfläche
eines schwarzen Lochs!
Eine genauere Rechnung mit Methoden der
Quantenfeldtheorie[1] liefert
anstelle des Proportionalitätsfaktors ![]() einen Faktor
einen Faktor ![]() und damit die vielfach publizierte Formel für die Entropie
eines schwarzen Lochs:
und damit die vielfach publizierte Formel für die Entropie
eines schwarzen Lochs:
![]()
![]()
[1]
Der Zusammenhang ![]() gilt in einer Euklid’schen Geometrie,
nicht aber für ein schwarzes Loch! Das heuristische Ergebnis einer proportional
mit der Fläche wachsenden Entropie aber gilt bei strengerer Rechnung auch und
liefert dann den um
gilt in einer Euklid’schen Geometrie,
nicht aber für ein schwarzes Loch! Das heuristische Ergebnis einer proportional
mit der Fläche wachsenden Entropie aber gilt bei strengerer Rechnung auch und
liefert dann den um ![]() größeren Faktor.
größeren Faktor.
Das entscheidende Ergebnis unserer Betrachtung ist, dass zum Ende des Kosmos nach Ausschöpfen der gravitativen Freiheitsgrade nurmehr stationäre Schwarze Löcher existieren, deren Temperatur nach dem Aufsaugen aller erreichbaren Materie nicht mehr sinken kann. Dieses wichtige Ergebnis folgt aus sehr allgemeinen Annahmen:
- Die Wirkung der Gravitation sinkt im gleichen Ausmaß, wie der Raum wächst.
- Aus der Quantennatur der Materie folgt eine Ortsunschärfe, die durch die Massenwellenlänge gegeben ist.
- Die minimale Informationsmenge ist 1 Bit und die minimale Entropiemenge 1.
Allein aus 1. folgt bereits die Existenz eines zur Masse proportionalen Ereignishorizonts. Allein aus 2. folgt bereits der Massenzuwachs eines schwarzen Lochs beim Verschwinden eines Probekörpers: umgekehrt proportional zum Ereignishorizont und unabhängig von der Masse des Probekörpers.
Könnten andere Teilchen mit Masse m und einer komplizierten inneren Struktur auf einem anderen Weg hinter dem Horizont verschwinden und möglicherweise mehr Entropie aus dem System herausnehmen? Es gäbe dann schwarze Löcher mit gleicher Masse, aber unterschiedlicher Entropie. Das ist aber unmöglich, da schwarze Löcher nur einen[7] Parameter, nämlich ihre Masse, haben.

Das Verschwinden einer Masse ![]() in einem schwarzen Loch:
in einem schwarzen Loch:
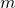 ist sehr weit[8]
entfernt
ist sehr weit[8]
entfernt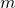 ruht[9] am Rand des
Ereignishorizonts
ruht[9] am Rand des
Ereignishorizonts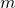 ist hinter dem Ereignishorizont verschwunden
ist hinter dem Ereignishorizont verschwunden
In einem expandierenden Kosmos sinkt die Temperatur der Hintergrundstrahlung permanent. Die Masse eines schwarzen Lochs aber ändert sich nicht mehr, wenn alle Materie aufgesaugt[10] ist.
Damit folgt, dass jedes schwarze Loch, egal wie groß, irgendwann ein Alter erreicht, in dem es wärmer als der leere Kosmos ist: es muss verdampfen! Virtuelle Teilchen-Antiteilchenpaare am Ereignishorizont werden getrennt, und der Temperaturunterschied verursacht eine Asymmetrie: das wärmere schwarze Loch dampft mehr Teilchen ab, als es von der kälteren Umgebung empfängt.
Das Ende des Kosmos
- Nachdem (fast) alle Materie in schwarzen Löchern verschwunden ist, verdampfen diese irgendwann und hinterlassen überwiegend Photonen und Gravitonen, ein paar Neutrinos und wenige andere massive Teilchen.
- Nachdem das letzte schwarze Loch verdampft ist, vielleicht nach 10100 Jahren, besteht der Kosmos ausschließlich aus masselosen Photonen, wenigen anderen massiven Verdampfungsprodukten und einigen Asteroiden, Planeten, und Sternresten – kalte Brocken, die schnell genug waren, dem Hunger der schwarzen Löcher zu entfliehen und als glückliche‘ Überbleibsel einer vergangenen Zeit mit der Expansion des Kosmos im Unendlichen verschwinden.
Das nur mit Strahlung erfüllte leere[11] Universum gleicht einem Schwarzen Körper und besitzt eine Entropie der Größe
![]()
Wie skalieren Temperatur und Entropie mit der Ausdehnung eines mit Schwarzkörperstrahlung erfüllten Hohlraums?
Die Entropie wächst bei gegebener Temperatur
proportional zum Volumen. Andererseits steckt die Entropie in der Strahlung.
Damit ist ![]() , also
, also ![]() . Die
Wellenlänge der Strahlungsphotonen aber ist proportional zur Ausdehnung des
Kosmos.
. Die
Wellenlänge der Strahlungsphotonen aber ist proportional zur Ausdehnung des
Kosmos.
Eine Reskalierung aller Längenmaße im
Universum lässt daher den Faktor ![]() und damit die Entropie
unverändert!
und damit die Entropie
unverändert!
Dies gilt auch für einen beliebig großen
Faktor, nehmen wir ![]() . Plötzlich erscheint das leere Universum am
Ende genau so, wie es bereits zu Anfang einmal war! Alles, was am Anfang des
Kosmos möglich war, ist auch am Ende wieder möglich. Und alles, was möglich
ist, wird in der Ewigkeit zur Gewissheit.
. Plötzlich erscheint das leere Universum am
Ende genau so, wie es bereits zu Anfang einmal war! Alles, was am Anfang des
Kosmos möglich war, ist auch am Ende wieder möglich. Und alles, was möglich
ist, wird in der Ewigkeit zur Gewissheit.
Ein neuer kosmischer Zyklus kann beginnen.
Irgendwann in der riesigen Zeitspanne zwischen Anfang und Ende des Kosmos wird es vielleicht wieder einen Wimpernschlag geben, der denkenden Wesen ein Bewusstsein schenkt.
So besteht das Universum aus einer Vielzahl nicht verknüpfter Welten, die unabhängig voneinander existieren und den gleichen Gesetzen folgen.
Wir haben damit ein Multiversum, bestehend aus voneinander vollständig entkoppelten Einzeluniversen. Und jedes von ihnen folgt derselben Mathematik, derselben Logik, derselben Harmonie!
Aber realisiert auch jede Welt die gleichen Dinge?
[1] Zur Vereinfachung der Schreibweise verwenden wir im Folgenden universelle Einheiten. Damit bekommen Lichtgeschwindigkeit ![]() , Gravitationskonstante
, Gravitationskonstante ![]() , Entropiequotient
, Entropiequotient ![]() und Wirkungsquantum
und Wirkungsquantum ![]() den Wert
den Wert ![]() .
.
[2]
Mit der Fluchtgeschwindigkeit gleicht die kinetische der potentiellen Energie
und es gilt ![]()
[3] Die Massenwellenlänge ![]() ist ein Maß für die Ortsunschärfe aufgrund der quantenmechanischen Wellennatur des Teilchens. Sie erscheint zB in der relativistischen Wellengleichung für Bosonen
ist ein Maß für die Ortsunschärfe aufgrund der quantenmechanischen Wellennatur des Teilchens. Sie erscheint zB in der relativistischen Wellengleichung für Bosonen ![]()
[4] Eine halbe Ortsunschärfe über dem Ereignishorizont
[5]
Wir erinnern uns: für den betrachteten Vorgang ist ![]() !
!
[6] Der Zusammenhang ![]() gilt in einer Euklid’schen Geometrie, nicht aber für ein schwarzes Loch! Das heuristische Ergebnis einer proportional mit der Fläche wachsenden Entropie aber gilt bei strengerer Rechnung auch und liefert dann den um
gilt in einer Euklid’schen Geometrie, nicht aber für ein schwarzes Loch! Das heuristische Ergebnis einer proportional mit der Fläche wachsenden Entropie aber gilt bei strengerer Rechnung auch und liefert dann den um ![]() größeren Faktor.
größeren Faktor.
[7] Wir verzichten in unserer konzeptionellen Diskussion auf die Betrachtung von rotierenden oder geladenen schwarzen Löchern: sie würde zum gleichen Ergebnis führen.
[8] Die Anziehung des schwarzen Lochs ist dort nicht mehr messbar.
[9] Was ist eine ‚eine am Ereignishorizont ruhende Punktmasse‘? Wir lassen sie an
einem langen, dünnen Faden, der weit draußen festgehalten wird, zum Horizont
hinab und kurz davor anhalten. Im Moment der Aufnahme von Teilbild 1 lassen wir
den Faden verschwinden. Wenn das schwarze Loch sehr groß ist, muss der Faden
nicht besonders stark sein. Das ruhende Teilchen hat nun noch die kurze Strecke
![]() zu fallen, bis es hinter dem Horizont verschwindet.
zu fallen, bis es hinter dem Horizont verschwindet.
[10] Das ‚Aufsaugen‘ kann sehr lange dauern, da Materie in einem ansonsten leeren Kosmos nur durch die Emission von Gravitationswellen ‚abgebremst‘ werden und sich dadurch dem Schwarzen Loch nähern kann.
[11] Irgendwann sind die Abstände zwischen benachbarten ‚Rest‘ – Massen so groß, dass sie kein Lichtsignal innerhalb jeder noch so großen ‚vernünftigen‘ Zeit verbinden kann: der Kosmos ‚zerfällt‘ in einzelne unabhängige Universen.
