Das Rätsel der Lichtgeschwindigkeit: wieso ändert sich diese nicht, wenn sich der Empfänger auf die Lichtquelle zu bewegt? Wieso bleibt sie unverändert gleich, im Fall, dass beide in Ruhe zueinander sind, und gleich auch für jede andere Bewegung?
Die immer gleichen Messergebnisse und die Konstanz der Lichtgeschwindigkeit sind ein Grundprinzip der Natur! Aus dieser Annahme und dem Relativitätsprinzip, nach dem ein gleichförmig bewegtes System einem ruhenden grundsätzlich gleicht, folgt für einen massiven Körper der Masse m
![]()
![]()
Fast jeder kennt diese Formel!
Schritt für Schritt lassen sich große Fragen der Physik lösen: warum besitzt ein heißer Raum einen nur endlichen Energieinhalt, wo doch die Zahl der in ihm möglichen elektromagnetischen Eigenschwingungen unendlich ist? Weil jede Mode mit einem Mindestmaß an Energie geladen werden muss – oder leer bleiben! Das energetische Mindestmaß öffnet den Quanten die Tür zur Physik, und alles wird damit anders werden.
Doch gemach, ein Schritt nach dem anderen.
Aus den Gleichungen für die Dynamik bewegter Ladungen und dem Verhalten elektrischer und magnetischer Felder ergibt sich die Ausbreitung des Lichts als Welle, und deren Lichtgeschwindigkeit. Doch kein System, in dem sie gemessen werden kann. Also muss sie in allen Systemen gelten, und überall gleich sein! Mit ![]() und der Quantisierung des elektromagnetischen Felds wird das Licht zu Teilchen, also ist es beides, Teilchen und Welle zugleich. Die Teilchen folgen einer Wellengleichung:
und der Quantisierung des elektromagnetischen Felds wird das Licht zu Teilchen, also ist es beides, Teilchen und Welle zugleich. Die Teilchen folgen einer Wellengleichung:
![]()
![]()
Die Bewegungsgleichung für quantenmechanische Observable steht in einem engen Zusammenhang mit der kanonischen Funktion, mit der die Bewegungsgleichungen der klassischen Mechanik hergeleitet werden können.
Die kanonische Funktion ![]() eines Systems von Teilchen beschreibt die Gesamtenergie als Funktion der Ortskoordinaten
eines Systems von Teilchen beschreibt die Gesamtenergie als Funktion der Ortskoordinaten ![]() und Impulskoordinaten
und Impulskoordinaten ![]() .
.
Von besonderem Interesse ist der Ausdruck
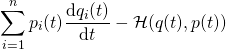
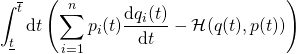
![]()
Für eine beliebige Kurve ![]() lautet das
vollständige Differential nach dem Parameter
lautet das
vollständige Differential nach dem Parameter ![]()
![]()
Für physikalische Bewegungen gelten die kanonischen Bewegungsgleichungen, und damit
![]()
![]()
![]()
![]()
Betrachten wir die Phasenraumkoordinaten selbst als Koordinatenfunktionen, so gilt für sie ![]() und
und ![]() , und für die klassische Mechanik gilt in Schreibweise der Poisson-Klammern
, und für die klassische Mechanik gilt in Schreibweise der Poisson-Klammern
![]()
![]()
![]()
![]()
![]()
Nun zu einem Beispiel: Betrachten wir einen Massenpunkt im Potential V, so erhalten wir
![]()
![]()
![]()
![]()
![]()
Die Quantenmechanik basiert auf den kanonischen Bewegungsgleichungen der Mechanik und damit auf dem Prinzip der stationären Wirkung, und gleichzeitig ist sie eine Wellengleichung! Die Brücke von der klassischen zur Quantenmechanik ist gefunden!
Aber Achtung: die Wellengleichung basiert auf einem Ausdruck für die Energie, der nur in einem, ausgezeichneten, Bezugssystem gilt. Die Konstanz der Lichtgeschwindigkeit aber verlangt nach einer Formulierung der Physik, die in allen und beliebig bewegten Bewegungssystemen gilt. Sie kann damit nur näherungsweise richtig sein und gilt ganz gut, wenn Geschwindigkeiten weit unterhalb der des Lichts bleiben.
Die Lösung für ein freies Teilchen ist
![]()
Viele Eigenschaften des Wasserstoffatoms werden erklärt:
Eine punktförmige geladene Masse, das Elektron, bewegt sich im radialsymmetrischen Feld einer Punktladung, dem Proton. Die Suche nach stabilen Zuständen mit Energie E führt auf die Wellengleichung für das Wasserstoffatom:
![]()
Wir wählen ein sphärisches Koordinatensystem
![]()
und erkennen, dass die gesuchte Wellenfunktion nur vom Abstand des Elektrons r und einem Polarwinkel ϑ abhängen kann und erhalten nach einer Separation der Variablen zwei lösbare Differentialgleichungen in je einer Variablen:
![]()
![]()
Die winkelabhängige Gleichung hat als Lösungen die Legendre-Funktionen
![]()
![Rendered by QuickLaTeX.com \[= \sqrt { \frac { ( l - m ) ! } { ( l + m ) ! } } \cdot \frac { 2 l + 1 } { 4 \pi } \cdot P _ { l } ^ { m } ( \cos \vartheta ) e ^ { i m \varphi }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-f9fc003ae535b3690abaa1f880a1b366_l3.png)
![]()
Mit
Parametern ![]() und
und ![]() . Es zeigt sich, dass
. Es zeigt sich, dass ![]() den Drehimpuls und
den Drehimpuls und ![]() dessen z-Komponente beschreibt. Die ersten
Lösungen lauten konkret
dessen z-Komponente beschreibt. Die ersten
Lösungen lauten konkret
![]()
![]()
![]()
![]()
![]()
Die Radialgleichung bei gegebenem Drehimpuls l lautet nun
![]()
Diese
Differentialgleichung wird durch die Laguerrefunktionen gelöst. Die
Grobstruktur der Spektrallinien wird berechenbar, die experimentell bestimmte
Balmer-Formel für den Abstand der Spektrallinien ![]() folgt sofort.
folgt sofort.
Die
Aufenthaltswahrscheinlichkeiten des Elektrons folgt in ihrer Winkelabhängigkeit
aus der mathematischen Struktur der Legendre-Funktionen und in ihrer radialen
Abhängigkeit den Laguerre-Funktionen: für ![]() zum Beispiel
heißt die Wellenfunktion (in ‚atomic units‘)
zum Beispiel
heißt die Wellenfunktion (in ‚atomic units‘)
![]()
Und das Quadrat dieses Ausdrucks gibt die Wahrscheinlichkeitsdichte für den Aufenthalt des Elektrons am Ort ![]() normiert auf das Volumen
normiert auf das Volumen ![]() (
(![]() entspricht dem Radius der ersten Elektronenbahn). Veranschaulicht ergibt sich eine Hantel:
entspricht dem Radius der ersten Elektronenbahn). Veranschaulicht ergibt sich eine Hantel:

Jetzt lassen sich bereits näherungsweise die ‚Atomorbitale‘ berechnen, nämlich die Aufenthaltswahrscheinichleiten für Elektronen mit anderen Kombinationen von ![]() – wenn man die Regel verstünde, nach der sich mehrere Elektronen in einem radialsymmetrisch proportional zum Abstand abfallenden Potential anordnen. Die Systematik der atomaren Spektrallinien lässt sich durch ein Ausschlussprinzip erklären: jeder Zustand mit einem bestimmten
– wenn man die Regel verstünde, nach der sich mehrere Elektronen in einem radialsymmetrisch proportional zum Abstand abfallenden Potential anordnen. Die Systematik der atomaren Spektrallinien lässt sich durch ein Ausschlussprinzip erklären: jeder Zustand mit einem bestimmten ![]() darf nur von je einem Elektron mit positivem und einem mit negativem Spin besetzt werden. Damit bereits liegt der Aufbau aller Elemente prinzipiell fest: die Orbitale werden sukzessive aufgefüllt, beginnend mit dem energetisch niedrigsten Orbital
darf nur von je einem Elektron mit positivem und einem mit negativem Spin besetzt werden. Damit bereits liegt der Aufbau aller Elemente prinzipiell fest: die Orbitale werden sukzessive aufgefüllt, beginnend mit dem energetisch niedrigsten Orbital ![]() , dem Grundzustand des Wasserstoffatoms.
, dem Grundzustand des Wasserstoffatoms.

Aus dem Aufbau der Elemente erklärt sich das Funktionieren der Chemie, und damit auch fast die gesamte Vielfalt aller im Kosmos vorhanden Dinge. Was heiß nun ‚fast‘? Jedenfalls alle für die Menschen im täglichen Leben wahrnehmbaren und sowieso alle ihren evolutiven Vorgängern erscheinenden Dinge und Wesen. Australopithecus Afarenis interessierte sich noch nicht für den Beta-Zerfall des isolierten Neutrons und baute auch keine Kernreaktoren. Dort aber wirken Kräfte, die auch die Existenz von vielfach positiv geladenen Atomkernen begründen. Wir haben sie zunächst vereinfachend vorausgesetzt und unsere Betrachtungen mit einem positiv geladenen und in guter Näherung punktförmigen Atomkern begonnen, dessen elektrisches Potential mit 1/r abfällt.
Warum aber gilt das Ausschlussprinzip , warum darf jeder Zustand mit einem bestimmten ![]() nur von je einem Elektron mit positivem und einem mit negativem Spin besetzt werden? Und was ist überhaupt Spin?
nur von je einem Elektron mit positivem und einem mit negativem Spin besetzt werden? Und was ist überhaupt Spin?
Wenn punktförmige Teilchen Ladung tragen und einen Drehimpuls, divergieren die klassischen Betrachtungen ins Unendliche.
Versuchen wir mit einer besseren Wellengleichung eine Antwort zu finden und verwenden als Ausgangspunkt den relativistischen Energie-Impuls Zusammenhang
![]()
also
![]()
Eine Anwendung der kanonischen Quantisierungsregeln verlangt, die Wurzel aus einem Differentialoperator zu ziehen! Wie soll das gehen?
Man könnte für die Anwendung der kanonischen Quantisierung direkt E2 ausgehen, dann wäre die Quantisierung klar und das Quadrat entspräche einer zweiten Ableitung. Eine auf diese Weise ‚relativistisch richtig‘ verbesserte Wellengleichung hätte die Form
![]()
Nun aber entsteht ein konzeptionelles Problem: die Differentialgleichung ist nicht mehr in erster Ordnung für die zeitliche Entwicklung! Von einer Wellenfunktion ![]() ausgehend ergibt sich deren Entwicklung in der Zeit nach der alten Wellengleichung eindeutig: wenn ich nur hinreichend kleine Zeitintervalle
ausgehend ergibt sich deren Entwicklung in der Zeit nach der alten Wellengleichung eindeutig: wenn ich nur hinreichend kleine Zeitintervalle ![]() hintereinanderreihe und die ‚Bewegung‘ der Wellenfunktion linear entwickle, erhalte ich aus der Gegenwart
hintereinanderreihe und die ‚Bewegung‘ der Wellenfunktion linear entwickle, erhalte ich aus der Gegenwart ![]() die Zukunft
die Zukunft ![]() . So ist die Quantenmechanik gewollt: es soll Zustände geben, deren gesamte Information in einer Wellenfunktion
. So ist die Quantenmechanik gewollt: es soll Zustände geben, deren gesamte Information in einer Wellenfunktion ![]() kodiert ist. Das funktioniert aber jetzt nicht mehr, da die neue Gleichung die zweite Ableitung nach der Zeit enthält. Um die Zukunft zu bestimmen, muss nun nicht mehr nur die Funktion
kodiert ist. Das funktioniert aber jetzt nicht mehr, da die neue Gleichung die zweite Ableitung nach der Zeit enthält. Um die Zukunft zu bestimmen, muss nun nicht mehr nur die Funktion ![]() bekannt sein, sondern auch noch deren Ableitung in der Zeit! Beides zusammen wäre schon denkbar, führt aber bei unserer einfachen Betrachtung zu einem Versickern der Wahrscheinlichkeit ins Unbekannte.
bekannt sein, sondern auch noch deren Ableitung in der Zeit! Beides zusammen wäre schon denkbar, führt aber bei unserer einfachen Betrachtung zu einem Versickern der Wahrscheinlichkeit ins Unbekannte.
Eine Anmerkung sei erlaubt:
Die Nutzung der in E quadratischen Gleichung ist nicht ganz sinnlos, sie führt zu
![]()
wo ![]() den d’Alembert Operator bezeichnet. Diese Gleichung gilt für Photonen. Die aber haben die Ruhemasse Null. Für sie gilt der besonders einfache Energie-Impuls Zusammenhang
den d’Alembert Operator bezeichnet. Diese Gleichung gilt für Photonen. Die aber haben die Ruhemasse Null. Für sie gilt der besonders einfache Energie-Impuls Zusammenhang
![]()
Und außerdem
wissen wir bereits, dass Photonen mit einem Impuls ![]() durch eine ebene Welle
durch eine ebene Welle ![]() beschrieben werden.
beschrieben werden.
Wir könnten nun auch zeigen, wie andere Feldteilchen mit ganzzahligem Spin derselben Gleichung wie die Photonen genügen, stellen dies aber zurück. Für ein Verständnis des Aufbaus der Dinge brauchen wir außer dem Photon keine weiteren Feldteilchen.
Was aber gilt für das Elektron?
Wir wollen einen linearen Zusammenhang ‚einfach‘ verlangen und haben das Glück, dass die Mathematik dafür die richtigen Zahlen bereithält:
![]()
Wir haben
den Ausgangspunkt durch Verwendung eines Maßstabs, in dem c = 1 wird,
vereinfacht und verlangen, dass die Wurzel einem linearen Ausdruck in ![]() entspricht:
entspricht:
![]()
![]()
Das Quadrieren und Ausmultiplizieren dieser einfachen Gleichung führt zur Forderung
![]()
![]()
Bereits
diese Forderung weist darauf hin, dass die seltsamen Zahlen ![]() mit
dem Verhalten von Objekten bei einer Drehung im dreidimensionalen Raum
zusammenhängen. Deshalb, zum Beispiel, genügen auch die Operatoren der
Komponenten des Drehimpulsvektors analogen Kommutationsbeziehungen.
mit
dem Verhalten von Objekten bei einer Drehung im dreidimensionalen Raum
zusammenhängen. Deshalb, zum Beispiel, genügen auch die Operatoren der
Komponenten des Drehimpulsvektors analogen Kommutationsbeziehungen.
Das Verhalten von Körpern bei Drehungen im Raum ist eine Fragestellung der Mathematik und unabhängig von den Dingen. Das Zahlensystem kann schrittweise erweitert werden, und führt in einer Folge von den natürlichen Zahlen über die rationalen Zahlen zu den reellen Zahlen und schließlich zu den erweitern komplexen Zahlen, die bereits in einer Ebene oder auf einer Kugeloberfläche visualisiert werden können. Jeder Schritt erweitert die Mathematik um ein unerschöpfliches Territorium für neue Entdeckungen und Zusammenhänge! Doch die Wirklichkeit des zeitlichen Erlebens ist dreidimensional! Wie kann die Mathematik von den zwei Dimensionen der komplexen Ebene so erweitert werden, dass sie auch höherdimensionale Anschauungen abbildet – und Drehungen leichter verständlich werden?
Der vierdimensionale Körper der Quaternionen löst das Problem. Neben der Eins bilden drei weitere Elemente i, j, k die Standardbasis der Quaternionen über dem Körper der reellen Zahlen, und diese genügen der Bedingung
![]()
Eine Drehung um den Winkel α im Euklidschen Anschauungsraum kann durch ein normiertes Quaternion qr dargestellt werden:
![]()
![]() ist der Einheitsvektor in der Drehachse.
ist der Einheitsvektor in der Drehachse.
Der Vektor
(1,0,0) repräsentiert das Quaternion ![]() und stellt eine Drehung von 180° um
die X-Achse dar, und (0,1,0) repräsentiert
und stellt eine Drehung von 180° um
die X-Achse dar, und (0,1,0) repräsentiert ![]() und eine Drehung von 180° um die
Y-Achse und
und eine Drehung von 180° um die
Y-Achse und ![]() eine Drehung von 180° um die Z-Achse. Somit entspricht
eine Drehung von 180° um die Z-Achse. Somit entspricht ![]() einer Drehung von 360° um die jeweilige Achse.
einer Drehung von 360° um die jeweilige Achse.
Die Quaternionen 1 und -1 entsprechen der Identitätsdrehung, bei der ein Objekt im dreidimensionalen Euklidschen Raum seine Lage nicht ändert. Ein Quaternion, das um 360° gedreht wird, ändert aber – genau wie auch ein Spinor – sein Vorzeichen! Und Spinoren sind genau die Zahlen, die wir für die Lösung der Wellengleichung brauchen!
Eine übliche Darstellung der Dirac-Spinoren verwendet die Generatoren der komplexen Drehgruppe SU(2). Wir haben sie als Pauli-Matrizen zitiert gefunden:
![]()
Sie besitzen die geforderten Eigenschaften:
![]()
![]()
![]()
![]()
Mit ihrer
Hilfe lassen sich die Komponenten des Vektors ![]() darstellen, die nun keine
Zahlen mehr, sondern 4×4 Matrizen sind:
darstellen, die nun keine
Zahlen mehr, sondern 4×4 Matrizen sind:
![Rendered by QuickLaTeX.com \[\alpha _ { x } = \left[ \begin{array} { c c c c } { 0 } & { 0 } & { 0 } & { 1 } \\ { 0 } & { 0 } & { 1 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 0 } & { 0 } \end{array} \right] \]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-6355e99a2cd9124b59b110ba8d76b011_l3.png)
![Rendered by QuickLaTeX.com \[\alpha _ { y } = \left[ \begin{array} { c c c c } { 0 } & { 0 } & { 0 } & { - i } \\ { 0 } & { 0 } & { i } & { 0 } \\ { 0 } & { - i } & { 0 } & { 0 } \\ { i } & { 0 } & { 0 } & { 0 } \end{array} \right]\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-84c5a3163b2bcf292b8b4914f839ca9b_l3.png)
![Rendered by QuickLaTeX.com \[\alpha _ { z } = \left[ \begin{array} { c c c c } { 0 } & { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } \\ { 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 0 } & { 0 } \end{array} \right]\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-565addfe9accc7b4a7456dcf0e4510e3_l3.png)
![Rendered by QuickLaTeX.com \[\beta = \left[ \begin{array} { c c c c } { 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } \end{array} \right]\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-10fe81e91e59c69d7851c71ba10a6e54_l3.png)
Damit lautet die Wellengleichung für ein freies Elektron nun
![]()
Lösungen dieser Gleichung für ein Elektron mit einem definierten Impuls p und einer Energie E sind
![Rendered by QuickLaTeX.com \[\psi_{1} = \left[ \begin{array} { c } { 1 } \\ { 0 } \\ { 0 } \\ { \frac { p _ { x } } { E + m } } \end{array} \right] e ^ { i \left( p _ { x } x - E t \right) }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-0df213639540619307084719e173b3b6_l3.png)
![Rendered by QuickLaTeX.com \[\psi_{2} = \left[ \begin{array} { c } { 0 } \\ { 1 } \\ { p _ { x } } \\ { \frac { p _ { x } } { E + m } } \\ { 0 } \end{array} \right] e ^ { i \left( p _ { s } x - E t \right) }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-9d01ac03aab2f78281c2a80aa9a1c35d_l3.png)
mit
![]()
Wieder
bedeutet ![]() die Aufenthaltswahrscheinlichkeit des
Elektrons in einem Volumenelement
die Aufenthaltswahrscheinlichkeit des
Elektrons in einem Volumenelement ![]() am Ort
am Ort ![]() .
.
Was aber bedeuten die vier Komponenten? Sie deuten darauf hin, dass ein Elektron in 4 unterschiedlichen ‚Varianten‘ existiert, also ‚innere‘ Freiheitsgrade besitzt!
Aufgrund der Gemeinsamkeiten zu den Pauli-Matrizen erkennt man, dass eine Dimension auf einen intrinsischen Drehimpuls hinweist, den Spin des Elektrons. Die Wellengleichung für das Wasserstoffatom lautet
![]()
Dabei ist ![]() die elektrische Feinstrukturkonstante[1].
die elektrische Feinstrukturkonstante[1].
Wie zuvor, bei der nichtrelativistischen Wellengleichung, werden die Lösungen durch Quantenzahlen parametrisiert. Diesmal aber ist nicht der Bahndrehimpuls L des Elektrons, sondern der Gesamtdrehimpuls J eine Erhaltungsgröße, und ein bestimmter Zustand ist durch die Quantenzahlen n, j, mj charakterisiert. Für dessen Energie gilt
![Rendered by QuickLaTeX.com \[E _ { n j } = \frac { m } { \sqrt { 1 + \frac { \alpha ^ { 2 } } { \left[ n - j - \frac { 1 } { 2 } + \sqrt { \left( j + \frac { 1 } { 2 } \right) ^ { 2 } - \alpha ^ { 2 } } \right] ^ { 2 } } } }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-5d98cfc4b31f068c27925a239114ddaa_l3.png)
![]()
Der erste Term m bezeichnet die Ruheenergie eines freien, ungebundenen Elektrons (E = mc2 mit c = 1!).
Der zweite Term ![]() ist identisch mit der Lösung aus der nichtrelativistischen Wellengleichung und bezeichnet die Energieniveaus der Balmerserie.
ist identisch mit der Lösung aus der nichtrelativistischen Wellengleichung und bezeichnet die Energieniveaus der Balmerserie.
Der nächste Term ![]() ist neu, und verweist auf die Überlegenheit der verbesserten Wellengleichung : er erklärt die Feinstruktur des Wasserstoffspektrums bereits recht gut!
ist neu, und verweist auf die Überlegenheit der verbesserten Wellengleichung : er erklärt die Feinstruktur des Wasserstoffspektrums bereits recht gut!
Es gibt aber noch zwei weitere Lösungen der Wellengleichung eines freien Elektrons, und diese liefern den Schlüssel zum Verständnis der Bedeutung der anderen zwei inneren Freiheitsgrade von ![]() :
:
![Rendered by QuickLaTeX.com \[\psi_{3} = \left[ \begin{array} { c } { 0 } \\ { - p _ { x } } \\ { | E | + m } \\ { 1 } \\ { 0 } \end{array} \right] e ^ { i \left( p _ { i } , x - E t \right) }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-734fff643bcf3365b093a54c6462630c_l3.png)
![Rendered by QuickLaTeX.com \[\psi_{4} = \left[ \begin{array} { c } { - p _ { x } } \\ { | E | + m } \\ { 0 } \\ { 0 } \\ { 1 } \end{array} \right] e ^ { i \left( p _ { x } x - E t \right) }\]](https://lastlog.cloud/wp-content/ql-cache/quicklatex.com-43775571658c16c657f9f37957d3ed25_l3.png)
und ![]()
Es sind Zustände mit negativer Energie!
Wir identifizieren diese Zustände mit den Antiteilchen, also Positronen. Ein Positron entspricht einem ‚fehlenden‘ Elektron mit negativer Energie, hat selbst also positive Energie. Das Zusammentreffen eines Positrons, also einem ‚fehlenden‘ Elektron und einem ‚normalen‘ Elektron führt erwartungsgemäß zur Auslöschung der Teilchen und lässt nur deren Energie übrig, die der doppelten Ruhemasse eines Elektrons entspricht. Der beim Zerfall eines Positronium[2]‚Atoms‘ beobachtbare Lichtblitz mit 2 x 511 keV Energie ist ein Beweis für die reale Existenz derartiger Vorgänge: Ruhemasse verschwindet, der Energiesatz gilt.
Spinoren haben ein interessantes Verhalten bei Drehungen im dreidimensionalen Euklidschen Raum: sie wechseln bei einer Drehung um 360° ihr Vorzeichen: ![]() wird zu
wird zu ![]() ! Das stört zunächst nicht, da nur das Betragsquadrat
! Das stört zunächst nicht, da nur das Betragsquadrat ![]() in die Aufenthaltswahrscheinlichkeit eingeht. Es ist aber extrem wichtig bei der Anwesenheit mehrerer Teilchen, bei der sich zunächst deren Wahrscheinlichkeitsamplituden überlagern und dann erst das Betragsquadrat gebildet wird. Ein Elektron, dessen Wellenfunktion im Euklidschen Raum um 360° gedreht wird, erreicht die gleiche Stelle wie zuvor, bekommt aber ein negatives Vorzeichen. Die Konsequenz könnte nicht dramatischer sein: für zwei identische Elektronen am gleichen Ort gilt
in die Aufenthaltswahrscheinlichkeit eingeht. Es ist aber extrem wichtig bei der Anwesenheit mehrerer Teilchen, bei der sich zunächst deren Wahrscheinlichkeitsamplituden überlagern und dann erst das Betragsquadrat gebildet wird. Ein Elektron, dessen Wellenfunktion im Euklidschen Raum um 360° gedreht wird, erreicht die gleiche Stelle wie zuvor, bekommt aber ein negatives Vorzeichen. Die Konsequenz könnte nicht dramatischer sein: für zwei identische Elektronen am gleichen Ort gilt ![]() ! Das ist nur mit
! Das ist nur mit ![]() erfüllbar: die Wahrscheinlichkeit, dass sich zwei identische Elektronen am gleichen Ort befinden ist Null! Hier liegt der Ursprung des ad-hoc geforderten Ausschließungsprinzips, und damit die Grundlage für die Stabilität und Form der Elemente und damit die Grundlage für alles Existierende im Kosmos! Der Ursprung der Dinge.
erfüllbar: die Wahrscheinlichkeit, dass sich zwei identische Elektronen am gleichen Ort befinden ist Null! Hier liegt der Ursprung des ad-hoc geforderten Ausschließungsprinzips, und damit die Grundlage für die Stabilität und Form der Elemente und damit die Grundlage für alles Existierende im Kosmos! Der Ursprung der Dinge.
Noch einmal zurück zur Wellengleichung: ![]() bewirkt eine unitäre Zeitentwicklung und bei abgeschlossenen Systemen mit Energieerhaltung gilt
bewirkt eine unitäre Zeitentwicklung und bei abgeschlossenen Systemen mit Energieerhaltung gilt
![]()
![]()
ein hermitescher unitärer Operator. Es gilt
![]()
Also
![]()
![]()
Ist ein System mit ![]() gegeben, so folgt dessen zeitliche Entwicklung deterministisch der Wellengleichung. Die zeitliche Richtung aber ist unbestimmt: das System ist in Bezug auf Zukunft und Vergangenheit symmetrisch.
gegeben, so folgt dessen zeitliche Entwicklung deterministisch der Wellengleichung. Die zeitliche Richtung aber ist unbestimmt: das System ist in Bezug auf Zukunft und Vergangenheit symmetrisch.
Nun führt aber jede Symmetrie zu einem Erhaltungssatz. In zeitsymmetrischen Systemen ist die Entropie erhalten.
Die Wellengleichung kann das in der Realität beobachtete Entropiewachstum und den zweiten Hauptsatz der Thermodynamik nicht begründen! Welches physikalische Gesetz dann?
Wir müssen diese Frage zunächst noch offen lassen.
[1] Die elektrische Feinstrukturkonstante ![]() ist eine reelle Zahl, die
ist eine reelle Zahl, die ![]() hingegen sind Spinoren. Wir haben gefunden, dass beide zumeist mit dem griechischen Buchstaben alpha belegt werden.
hingegen sind Spinoren. Wir haben gefunden, dass beide zumeist mit dem griechischen Buchstaben alpha belegt werden.
[2] Das Proton eines Wasserstoffatoms wird durch ein Positron, also Antielektron, ersetzt.
